Inteligencia Lógico - Matemática

desarrollando el razonamiento lógico y el cálculo numérico

Para el desarrollo de esta competencia de manera lúdica podemos emplear dos juegos matemáticos.

Aquí os dejamos dos de ellos.

1. El cuadrado mágico 

2. La Torre de hanoi

El cuadrado  mágico:

El cuadrado mágico es una figura cuadrada de orden n x n, donde se distribuyen números de manera que la 

suma horizontal, vertical y diagonal siempre es una constante.

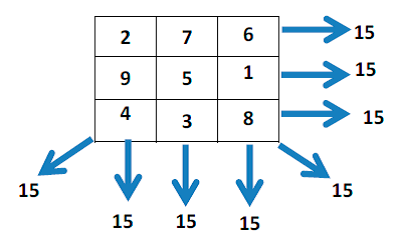
Un ejemplo:  Un cuadrado de orden 3 x 3 en donde filas, columnas y diagonales suman 15

 

¿Cómo completar un cuadrado mágico al que le faltan números?

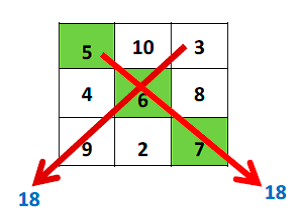
1. Observar la fila, columna o diagonal que esté completa. En este caso, la diagonal

2. Suma los dígitos de las casillas; ese resultado será tu constante.

    En este caso la constante es 18.

3. Ahora busca la fila, columna o diagonal con más datos. Súmalos y piensa

¿Cuánto te falta para llegar a tú constante?. El resultado será el número que completa esa casilla.

4. Repite el proceso hasta completar el cuadro.

5. Una vez completado tu cuadrado mágico, comprueba que las diagonales también sumen tu constante, en este caso: 18 

¿Para qué sirven los cuadrados mágicos en el aula de clase?

1. De forma lúdica y divertida los alumnos practican la suma y la resta, consolidando los procesos de adición y sustracción.

2. Utilizan estrategias de cálculo mental. Los chicos deben utilizar la lógica para detectar que número es la constante y con qué números deben trabajar para hallar los que les faltan.

3. Tienen que buscar regularidades dentro de los cuadrados.

4. Tienen que expresar verbalmente los procesos que han seguido para completar el cuadrado. 

5. Además, deben perseverar en la búsqueda de soluciones (realizan todos los intentos que sean necesarios hasta resolver el cuadrado.

 

¿Cómo construir cuadrados mágicos de orden impar?

Un ejemplo de estos cuadrados mágicos es el de orden  3 x 3, con números consecutivos del  1 al 9

METODO 1:

Consiste en ubicar el número 1 en la celda central de la primera fila de la tabla y luego completar, sucesivamente los números consecutivos en forma diagonal  ascendente, teniendo cuidado que si se sale de la tabla se considera dentro de la tabla de acuerdo a su ubicación. ¿Cómo?...

El siguiente Ejemplo te explica el procedimiento:

- Cuadrícula de 3 x 3

- Números: del 1 al 9                    

El resultado es un cuadrado mágico de 3 x 3, con números del  1 al 9 y cuya constante es 15

METODO 2

CUADRADO MÁGICO 3 X 3 CON NÚMEROS DEL 1 AL 9

1. Se dibuja la cuadrícula

2. Se agrega 1 cuadrícula a las celdas centrales de cada lado

3. Se colocan los números, siguiendo la misma dirección, sobre cada una de las diagonales en que hay tres cuadrados

4. Para colocar los números de las casillas externas dentro de los cuadrados:

            - el nº de la casilla externa superior pasa a la casilla vacía de abajo

- el nº de la casilla externa inferior  pasa a la casilla vacía de arriba

- el nº de la casilla externa de la derecha  pasa a la casilla vacía de la izquierda

- el nº de la casilla externa de la izquierda  pasa a la casilla vacía de la derecha

 

5. Comprobamos que todas las filas, columnas y diagonales del cuadrado sumen 15

Recuerda:

Todos los cuadrados mágicos de 3 x 3 tienen ocho soluciones, ya que se pueden escoger ocho formas diferentes de colocar la serie

¿Cómo calculamos la constante para los cuadrados mágicos más grandes?

Usando la fórmula matemática siguiente:

Ejemplo:

Si queremos calcular la constante matemática de un cuadrado mágico de orden 5 x 5:

 
En nuestro cuadrado mágico de orden 5 x 5, todas las filas, columnas y diagonales tendrían que sumar 65


¿Te gustó este post?, déjanos tus comentarios.

En la próxima entrada: Las torres de Hanoi