“El juego del fin del mundo”

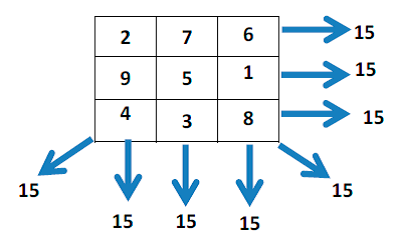
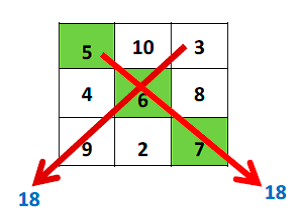
Como os comentamos en el post anterior, hoy os dejamos otro juego matemático para el desarrollo de la inteligencia lógico - matemática de manera lúdica: la Torre de Hanoi.

LA Torre de Hanoi : “El juego del fin del mundo”

Es un juego matemático que consiste en tres varillas verticales en las que se encuentran un número indeterminado de discos que determinarán la complejidad de la solución final.

Todos los discos son diferentes (no hay dos iguales) y van colocados ascendentemente, de mayor a menor, en la primera varilla (nunca se puede colocar un anillo mayor  o más grande sobre otro inferior o más pequeño).

El juego consiste en pasar todos los discos a la tercera varilla, colocados de la misma manera en que se inicia: de mayor a menor, ascendentemente.

Acerca de este jugo hay una leyenda que dice: “Al crear el mundo, Dios colocó tres varillas de diamante con 64 discos en la primera. También creó un monasterio de monjes y los mandó a resolver la Torre de Hanoi Divina . El día que estos monjes logren terminar el juego, el mundo acabará”. Sin embargo, las investigaciones han determinado que esta leyenda fue un invento publicitario del creador del juego, el matemático francés del siglo XVIII  Édouard Lucas que en aquella época se ganaba la vida vendiendo sus juegos matemáticos (lo cual era muy común en esa época).

 

 

 ¿Cómo se resuelve LA Torre de Hanoi?

Inteligencia Lógico - Matemática

desarrollando el razonamiento lógico y el cálculo numérico

Para el desarrollo de esta competencia de manera lúdica podemos emplear dos juegos matemáticos.

Aquí os dejamos dos de ellos.

1. El cuadrado mágico 

2. La Torre de hanoi

El cuadrado  mágico:

El cuadrado mágico es una figura cuadrada de orden n x n, donde se distribuyen números de manera que la 

suma horizontal, vertical y diagonal siempre es una constante.

Un ejemplo:  Un cuadrado de orden 3 x 3 en donde filas, columnas y diagonales suman 15

 

¿Cómo completar un cuadrado mágico al que le faltan números?

1. Observar la fila, columna o diagonal que esté completa. En este caso, la diagonal

2. Suma los dígitos de las casillas; ese resultado será tu constante.

    En este caso la constante es 18.

3. Ahora busca la fila, columna o diagonal con más datos. Súmalos y piensa

¿Cuánto te falta para llegar a tú constante?. El resultado será el número que completa esa casilla.

4. Repite el proceso hasta completar el cuadro.

5. Una vez completado tu cuadrado mágico, comprueba que las diagonales también sumen tu constante, en este caso: 18 

¿Para qué sirven los cuadrados mágicos en el aula de clase?